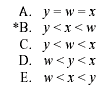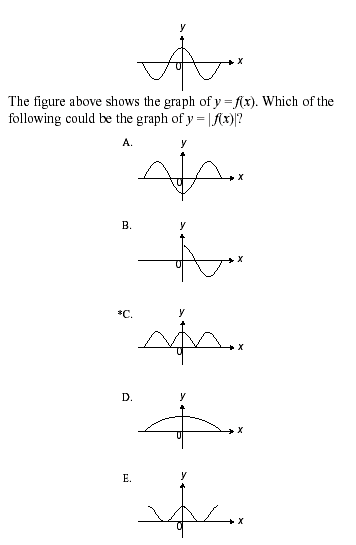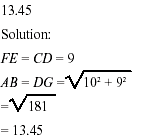Item Types
Central to the development of the NAEP assessment in mathematics is the careful selection of test questions or items to measure the content objectives and cognitive areas. The NAEP mathematics assessment consists of multiple-choice, short constructed-response, and extended constructed-response items. Examples of NAEP mathematics items for grades 4, 8, and 12 are provided below. Please refer to the NAEP Web site at www.nces.ed.gov/nationsreportcard for additional items, scoring rubrics, performance data, and sample student responses.
Grade 4
| 503 – 207 = A. 206 *B. 296 C. 304 D. 396 [Percent correct: 53%] |
| N stands for the number
of stamps John had. He gave 12 stamps to his sister. Which expression
tells how many stamps John has now? A. N + 12 *B. N – 12 C. 12 – N D. 12 x N [Percent correct: 67%] |
| In a bag of marbles, 1/2 are red, 1/4 are blue,
1/6 are green, and 1/12 are yellow. If a marble is taken from the
bag without looking, it is most likely to be *A. red B. blue C. green D. yellow [Percent correct: 25%] |
Grade 8
|
[Percent correct: 48%] |
|
Which of the following ordered pairs (x, y) is a
solution to the equation 2x – 3y = 6? [Percent correct: 41%] |
How many hours are equal to 150 minutes?
[Percent correct: 58%] |
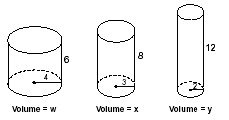 In the figures above, the radius and height of each right circular cylinder are given. If w, x, and y represent the volume of the cylinders, which of the following statements is true?
|
|
[Percent correct: 20%] D |
|
The length of a side of the square
above is 6. What is the length of the radius of the circle? |
Short Constructed-Response Items
To provide more reliable and valid opportunities for extrapolating about students’ approaches to problems, recent NAEP assessments have included items that are often referred to as constructed response or open ended. These short-answer items require students to give either a numerical result or the correct name or classification for a group of mathematical objects, draw an example of a given concept, or write a brief explanation for a given result.
Grade 4
Ms. Hernandez formed teams of 8 students each from the 34 students in her class. She formed as many teams as possible, and the students left over were substitutes.
How many students were substitutes?
Answer: ___________________
[Percent correct: 39%]
| Scoring Guide |
| Score and Description
Correct 2 Incorrect Incorrect response |
Grade 4
How many fourths make a whole?
Answer: ___________________
[Percent correct: 50%]
| Scoring Guide |
|
Score and Description
Incorrect Incorrect response |
Grade 8
From any vertex of a 4-sided polygon, 1 diagonal can be drawn.
From any vertex of a 5-sided polygon, 2 diagonals can be drawn.
From any vertex of a 6-sided polygon, 3 diagonals can be drawn.
From any vertex of a 7-sided polygon, 4 diagonals can be drawn.
How many diagonals can be drawn from any vertex of a 20-sided polygon?
Answer: ___________________
[Percent correct: 54%]
| Scoring Guide |
| Solution: 17 |
In this question a student needed to demonstrate an understanding
of diagonals of polygons. A diagonal of a polygon is a segment that joins
two nonadjacent vertices (a vertex is a common endpoint of two sides of
the polygon). To answer the question it was expected that a student would
observe that the number of diagonals from any vertex is 3 less than the
number of sides. That is, from any vertex of a convex polygon a diagonal
can be drawn to any of the other vertices of that polygon except the two
adjacent vertices. For a 20- sided polygon, the answer is 20 – 3 = 17.
| Scoring and Description |
| Correct Correct Response (17) Incorrect Any incorrect response |
Grade 8
Hair Color Survey Results
| Color of Hair | Percentage |
|---|---|
|
Blond
|
17
|
|
Brown
|
50
|
|
Black
|
33
|
|
Total
|
100
|
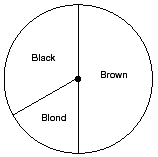
The table above shows the results of a survey of hair color. On the circle below, make a circle graph to illustrate the data in the table. Label each part of the circle graph with the correct hair color.
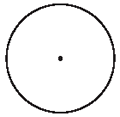
[Percent correct: 72%]
Grade 8
| Scoring Guide |
| Score and Description
The brown region should be about 1/2 of the circle. The blond region should be about 1/2 the black region. All three regions must be labeled with the correct colors or with the correct percents. Incorrect Incorrect answer |
Grade 12
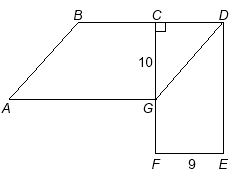
In the figure above, ABDG is a parallelogram and
CDEF is a rectangle.
If EF = 9 and CG = 10, what is AB to the nearest hundredth?
Answer: ___________________
(Students had access to a calculator.)
[Percent correct: 21%]
| Scoring Guide |
| Score and Description
Incorrect #1 Incorrect answer other than Incorrect #2 |
Extended Constructed-Response Items
Extended constructed-response items require students to consider a situation that demands more than a numerical or short verbal response. These items require the student to carefully consider a problem within or across the content strands, understand what is required to “solve” the problem, choose a plan of attack, carry out the attack, and interpret the solution in terms of the original problem. The response mode requires that students provide evidence of their work on some aspects of the problem-solving process and communicate their decisionmaking steps in the context of the problem.
Grade 4
Think carefully about the following question. Write a complete answer. You may use drawings, words, and numbers to explain your answer. Be sure to show all of your work.
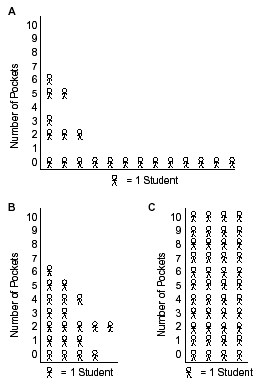
There are 20 students in Mr. Pang’s class. On Tuesday, most of the students in the class said they had pockets in the clothes they were wearing.
Which of the graphs most likely shows the number of pockets that each child had?
Explain why you chose that graph.
Explain why you did not choose the other graphs.
Scoring Guide
Solution:
Graph B because it had 20 students and most of the students
had pockets.
It could not be graph A because most of the students should have pockets.
It could not be graph C, since there are more than 20 students
shown.
OR
It is not likely that there would be the same number of students for each
number of pockets.
OR
Most clothes don’t have 10 pockets.
| Score and Description |
| Extended
The student chooses graph B and gives a good explanation why it should be B and explains why it can’t be A or C. The explanation must deal with both the number of students in the class and the fact that most of them have pockets. These explanations may occur in either response. Satisfactory The student chooses graph B and gives a good explanation
(which includes the fact that graph B has 20 students and most of
the students have pockets) but does not mention the other graphs. Partial The student chooses graph B but does not give an
adequate, relevant explanation.
Minimal
The student chooses graph B with no explanation or
a weak, nonrelevant (e.g., because it made sense) explanation.
Incorrect/Off Task The work is completely incorrect, irrelevant, or
off task.
|
[Extended 3%, Satisfactory 7%, Partial 15%, Minimal 23%]
Grade 8
This question requires you to show your work and explain your reasoning. You may use drawings, words, and numbers in your explanation. Your answer should be clear enough so that another person could read it and understand your thinking. It is important that you show all your work.
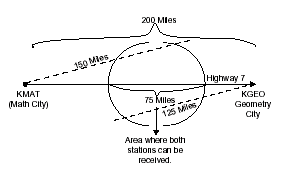
Radio station KMAT in Math City is 200 miles from radio station KGEO in Geometry City. Highway 7, a straight road, connects the two cities.
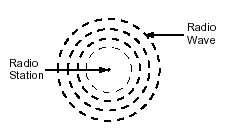 KMAT
broadcasts can be received up to 150 miles in all directions from the
station and KGEO broadcasts can be received up to 125 miles in all directions.
Radio waves travel from each radio station through the air, as represented
above.
KMAT
broadcasts can be received up to 150 miles in all directions from the
station and KGEO broadcasts can be received up to 125 miles in all directions.
Radio waves travel from each radio station through the air, as represented
above.
On the next page, draw a diagram that shows the following:
- Highway 7.
- The location of the two radio stations.
- The part of Highway 7 where both radio stations can be received.
 Scoring
Guide Solution:
Scoring
Guide Solution:
There is a 75-mile part of Highway 7 that is within both broadcast areas. It starts 75 miles outside Math City and ends 150 miles outside Math City.
| Score and Description |
| Extended
Correct answer. (75 miles must be stated.) Satisfactory Map with cities or stations and 200 miles labeled (or a clear and correct application of scale) and identifies common broadcast area on Highway 7 but omits length of common area. Partial Map with cities or stations and 200 miles labeled (or some attempt at using a scale): the highway should be shown as straight, and identifies incorrect common broadcast area (e.g. not on Highway 7) or insufficiently identifies an area. (Insufficiently means that there is not enough information labeled to determine the length of the common broadcast area.) Bounds of common area may or may not be labeled. Minimal Map with cities or stations and 200 miles labeled
(or some attempt to use a scale). Highway should be shown as straight.
There is no indication of how student determined common broadcast
area. (It may, for example, be represented as a single point or
not at all.)
Incorrect/Off Task The work is completely incorrect, irrelevant, or off task. |
Note:
A student’s map must include enough information concerning the lengths given in the question to justify that 75 miles is the common broadcast area. If pertinent information concerning lengths is missing, the maximum score that can be awarded is Partial.
[Extended 1%, Satisfactory 4%, Partial 13%, Minimal 22%]
Grade 12
This question requires you to show your work and explain your reasoning. You may use drawings, words, and numbers in your explanation. You answer should be clear enough so that another person could read it and understand your thinking. It is important that you show all your work.
The table below shows the daily attendance at two movie theaters for 5 days and the mean (average) and the median attendance.
| Theater A | Theater B | |
|---|---|---|
|
Day 1
|
100
|
72
|
|
Day 2
|
87
|
97
|
|
Day 3
|
90
|
70
|
|
Day 4
|
10
|
71
|
|
Day 5
|
91
|
100
|
|
Mean (average)
|
75.6
|
82
|
|
Median
|
90
|
72
|
(a) Which statistic, the mean or the median, would you use
to describe the typical daily
attendance for the 5 days at Theater A?
Justify your answer.
(b) Which statistic, the mean or the median, would you
use to describe the typical daily
attendance for the 5 days at Theater B?
Justify your answer.
Scoring Guide
Solution:
Selects and provides appropriate explanation for why the mean is a better measure for the typical attendance for Theater B and the median is the better measure for Theater A.
An explanation for Theater A should include the idea that the attendance on day 4 is much different than the attendance numbers for any other days for Theater A.
An appropriate explanation for Theater B should include the following ideas:
- There are two clusters of data.
- The median is representative of only one of the clusters while the mean is representative of both.
OR
- a justification that conveys the idea that 82 is a better indicator of where the "center" of the 5 data points is located
Scoring Guide
In this question, a student has to look at the data and determine which measure, the median or the mean, would best describe the typical daily attendance at each theater. A student has to have an understanding of the meaning of mean and median in order to provide a correct answer and explanation. For full credit, a student has to answer the median for part a and include an explanation that would include that day 4's attendance is significantly different than the rest of the days and the mean for part b with an explanation that shows an understanding that the mean is a better indicator because all of the attendance numbers for Theater B are clustered. Varying levels of partial credit (satisfactory, partial, and minimal) could be earned depending on how well the student reasons and communicates the correct answer.
| Score and Description |
| Extended
Indicates the better measure for each theater and gives a complete explanation for each measure. Satisfactory Indicates the better measure for each theater and gives a complete explanation for one measure. Partial Indicates mean for Theater B and median for Theater A with either no explanation or an incomplete explanation. OR The student selects the better measure for one theater and gives an appropriate explanation. Minimal Indicates the mean for Theater B with no explanation or an incomplete explanation. OR The student indicates the median for Theater A with no explanation or an incomplete explanation. Incorrect Incorrect response |
[Extended 1%, Satisfactory 3%, Partial 10%, Minimal 28%]
| Previous | Contents | Next |
|
|
|
| Mathematics Framework for the 2003 National Assessment of Educational Progress | |